Effektivzins - effektiver Jahreszins

Der Effektivzins stellt eine wichtige Größe bei der Bewertung von Finanzinvestitionen dar und bedient sich der internen Zinsfußmethode.

Der Effektivzins drückt dabei die Rentabilität für einen Kapitaleinsatz aus, indem sämtliche Zahlungen zu den jeweiligen Zeitpunkten berücksichtigt werden.

In den Wert für den Effektivzins sollten demnach sämtliche Kosten wie Gebühren, Agio bzw. Disagio, Zinszahlungen, Nominalzinssatz, Laufzeit, etc. eingehen. Hierbei kommt es insbesondere auch immer auf die jeweiligen Zeitpunkte an, zu denen bestimmte Zahlungen geleistet bzw. empfangen werden.

In § 4 der Preisangabenverordnung (PAngV) ist festgelegt, dass bei Krediten mit Festkonditionen ein effektiver Jahreszins vom Kreditanbieter angegeben werden muss. Bei einem Kredit mit variablen Konditionen ist der Effektivzins als anfänglicher effektiver Jahreszins anzugeben.

Interner Zinfuß als mathematischer Hintergrund

Die Effektivzins-Berechnung erfolgt dabei üblicherweise nach der Methode des internen Zinsfußes. In der Finanzmathematik ist dies der Zinsfuß, bei dem der auf den Kalkulationszeitpunkt bezogene Kapitalwert einer Investition gleich Null ist. Dies bedeutet, bezogen auf die jeweilige Investition, dass der Barwert aller Auszahlungen gleich dem Barwert aller Einzahlungen ist.

Als mathematische Formel ausgedrückt sieht dies so aus: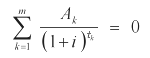

Die einzelnen Variablen haben folgende Bedeutung:

• k - die laufende Nummer des Zahlungstroms, von 1 bis m.
• m - Gesamtzahl der ein- und ausgehenden Zahlungsströme
• A_k - Betrag einer Zahlung zum Zeitpunkt t_k, dabei gilt:
  A_k > 0 bei einer eingehenden Zahlung,
  A_k < 0 bei einer ausgehenden Zahlung.
  Die Abfolge der Werte A_k stellt also eine Zahlungsreihe mit Ein- und Auszahlungen dar.
• t_k - Zeitpunkt des k-ten Zahlungsstroms in Jahren oder Jahresbruchteilen, wobei t₁ = 0.
• i - interner Zinsfuß, Effektivzins bzw. effektiver Jahreszins

Berechnungsmethode

Die zu errechnende Variable ist in unserem Fall der interne Zinfuß i. In der Regel ist es jedoch nicht möglich, diese Gleichung einfach nach i aufzulösen. Somit muss die Berechnung durch ein iteratives Näherungsverfahren erfolgen, mit dem sich der gesuchte interne Zinsfuß schrittweise annähern lässt.

Es sind jedoch Spezialfälle konstruierbar, in denen der interne Zinsfuß nicht berechnet werden kann, oder aber auch mehrere Lösungen für die o.g. Gleichung existieren. Für Investitionen, deren Zahlungsreihe nur einen Vorzeichenwechsel besitzen ist der interne Zinfuß in der Regel aber eindeutig bestimmbar.

Kritische Einschätzung

Für die Bedeutung die Effektivzinses nach dem internen Zinfußmethode ist noch wichtig zu wissen, dass diese eine Wiederanlageprämisse zum internen Zinsfuß impliziert. Dennoch ist der Effektivzins eine gute Bewertungsmöglichkeit für viele Finanzinvestitionen, insbesondere für Einzelinvestitionen.

Eine Investition kann somit für sich genommen als sinnvoll betrachtet werden, wenn der errechnete Effektivzins eine bestimmte gewünschte Mindestrendite erreicht bzw. übersteigt.